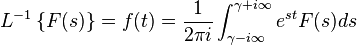Từ năm 1744, Leonhard Euler đã đưa ra các tích phân
 và
và 
để giải các phương trình vi phân.
Joseph Louis Lagrange, người rất ngưỡng mộ Euler, khi nghiên cứu cách tính tích phân của hàm mật độ xác suất, ông đã đưa ra biểu thức tích phân

Những dạng tích phân này đã thu hút sự chú ý của Laplace vào năm 1782 khi ông tiếp tục công trình của Euler là sử dụng phép tính tích phân để giải các phương trình. Năm 1785, vượt ra khỏi giới hạn giải quyết các phương trình bằng phương pháp tích phân, ông đã bắt đưa ra các biến đổi mà sau này đã trở nên rất phổ biến. Ông sử dụng tích phân

- tương tự với biến đổi Mellin, để biến đổi phương trình sai phân để tìm ra lời giải cho phương trình biến đổi. Với cách tương tự như vậy, ông đã suy ra các tính chất của biến đổi Laplace.
Laplace cũng nhận ra rằng phương pháp của Joseph Fourier trong chuỗi Fourier để giải phương trình khuếch tán chỉ có thể áp dụng trong một vùng không gian giới hạn.
Giả sử f là một hàm (có thể là hàm phức) của biến số thực t (t ≥ 0) sao cho tích phân  hội tụ ít nhất với một số phức s = a + ib, thì khi đó ảnh của hàm f qua biến đổi Laplace là hàm F được định nghĩa bởi tích phân sau
hội tụ ít nhất với một số phức s = a + ib, thì khi đó ảnh của hàm f qua biến đổi Laplace là hàm F được định nghĩa bởi tích phân sau

Một số trường hợp để đảm bảo cho cả những trường hợp hàm gốc f(t) không xác định tại t=0, ta có thể định nghĩa một cách chính xác hơn.

Một khi nói "biến đổi Laplace" mà không chú ý thêm gì, thường là ta nói đến biến đổi một phía. Biến đổi Laplace có thể được định nghĩa là biến đổi Laplace hai phía bằng cách mở rộng giới hạn của tích phân đến âm vô cực.
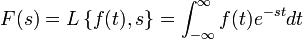
Nếu như vậy, biến đổi Laplace một phía đơn giản trở thành một trường hợp đặc biệt của biến đổi Laplace hai phía, xác định bằng cách lấy hàm đã chuyển đổi nhân với hàm bước nhảy Heaviside. than
Biến đổi Laplace ngược giúp chúng ta tìm lại hàm gốc f(t) từ hàm ảnh F(p). Biến đổi Laplace ngược được định nghĩa bởi tích phân sau.
Nhưng thông thường chúng ta ít dùng đến tích phân này để tính hàm gốc mà dùng bảng "các hàm gốc – hàm ảnh tương ứng" đã có sẵn để tìm lại hàm gốc f(t).
Tập hợp các hàm f của biến số thực t sao cho tích phân  hội tụ ít nhất với một số phức p gọi là lớp hàm gốc. Trong khi đó tập hợp các giá trị của p sao cho tích phân
hội tụ ít nhất với một số phức p gọi là lớp hàm gốc. Trong khi đó tập hợp các giá trị của p sao cho tích phân  tồn tại thì được gọi là miền hội tụ (hay miền qui tụ).
tồn tại thì được gọi là miền hội tụ (hay miền qui tụ).
Ta có thể chứng minh được lớp các hàm gốc phải thỏa mãn các tính chất sau.


| Tính chất | Miền thời gian | Miền tần số |
|---|---|---|
| Tuyến tính |  |  |
| Đạo hàm trong miền tần số | 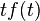 | 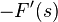 |
| Đạo hàm bậc n trong miền tần số | 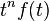 |  |
| Đạo hàm trong miền thời gian |  |  |
| Đạo hàm bậc 2 |  |  |
| Tổng quát |  |  |
| Tích phân trong miền tần số |  | 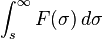 |
| Tích phân trong miền thời gian |  |  |
| Đồng dạng |  |  |
| Biến đổi trong miền tần số | 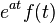 | 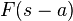 |
| Biến đổi trong miền thời gian |  | 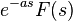 |
| Tích chập |  |  |
| Hàm tuần hoàn |  |  |
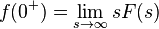
 , trong nửa mặt phẳng (Re.s > so)
, trong nửa mặt phẳng (Re.s > so)
- f(t) = 0, với mọi t < 0.
- Khi t ≥ 0, hàm f(t) liên tục cùng với các đạo hàm cấp đủ lớn trên toàn trục t, trừ một số hữu hạn điểm gián đoạn loại một.
- Khi
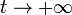 hàm f(t) có cấp tăng bị chặn, tức là tồn tại hằng số s>0 và M>0 sao cho
hàm f(t) có cấp tăng bị chặn, tức là tồn tại hằng số s>0 và M>0 sao cho  Khi đó so = inf {s} được gọi là chỉ số tăng của hàm f. (Tức là hàm f(t) không được tăng nhanh hơn hàm est để đảm bảo tích phân Laplace hội tụ).
Khi đó so = inf {s} được gọi là chỉ số tăng của hàm f. (Tức là hàm f(t) không được tăng nhanh hơn hàm est để đảm bảo tích phân Laplace hội tụ). - Cho các hàm f(t) và g(t), và các hàm ảnh tương ứng F(s) và G(s):
- Sau đây là bảng các tính chất của biến đổi Laplace:
- Định lý giá trị ban đầu: (Định lý giới hạn)
- Định lý giá trị cuối: (Định lý giới hạn)
- Tên file:
- Tài liệu về bài tập phần Laplace
- Phiên bản:
- N/A
- Tác giả:
- N/A
- Website hỗ trợ:
- N/A
- Thuộc chủ đề:
- Danh Mục » Ngành cơ điện tử » Kỹ thuật điều khiển tự động
- Gửi lên:
- 12/08/2013 07:10
- Cập nhật:
- 12/08/2013 07:10
- Người gửi:
- haihoang_boy
- Thông tin bản quyền:
- N/A
- Dung lượng:
- N/A
- Đã xem:
- 1556
- Đã tải về:
-
0
- Đã thảo luận:
- 0
Tài Liệu Mới Nhất
- Hệ Thống Máy Và Thiết Bị Lạnh - Pgs.Ts.Đinh Văn Thuận & Võ Chí Chính, 456 Trang
07.10.2016 09:10 - Giáo trình cảm biến công nghiệp - ĐHBK Đà Nẵng
27.09.2016 09:01 - Download phần mềm triển khai hình gò
26.08.2016 12:09 - Download Autocad 2017 Full Key Crack + Keygen + Hướng dẫn cài đặt
25.08.2016 09:50 - [Tài liệu] Vibration chart: Bảng tra các đồ thị rung động dạng phổ
20.08.2016 08:53 - [Tài liệu] Tìm hiểu đồ gá trên máy CNC - ĐHGTVT
18.08.2016 08:40 - [Tài liệu] Tổng quan về máy CNC và lập trình CNC cho máy phay, máy tiện
18.08.2016 08:25 - Giáo trình Maintenance Engineering Handbook
16.08.2016 08:43 - Strategic Six Sigma - Best Practices from the Executive Suite
15.08.2016 04:54 - Handbook On Green Productivity
15.08.2016 04:49